Сначала займёмся повторением
Ответы к с. 9
11. Периметр квадрата равен 32 дм. На сколько квадратных дециметров увеличится площадь квадрата, если его периметр увеличить на 12 дм?
1) 32 : 4 = 8 (дм) — сторона исходного квадрата
2) 8 • 8 = 64 (кв. дм) — площадь исходного квадрата
3) 32 + 12 = 44 (дм) — периметр нового квадрата
4) 44 : 4 = 11 (дм) — сторона нового квадрата
5) 11 • 11 = 121 (кв. дм) — площадь нового квадрата
×11
11
+11
11
121
6) 121 — 64 = 57 (кв. дм)
О т в е т: площадь квадрата увеличится на 57 кв. дм.
12. Измерь с помощью палетки площадь данного прямоугольника.
Палетку надо совместить с контуром прямоугольника так, чтобы стороны палетки с цифрами совпали со сторонами прямоугольника и квадраты палетки полностью расположились в прямоугольнике. Площадь прямоугольника 15 кв. см.
13. На сколько минутных делений должна повернуться минутная стрелка, чтобы получился поворот на прямой угол? Какую часть прямого угла составляет угол, на который поворачивается минутная стрелка за 5 мин?
На 15 минутных делений. Одну треть (третью часть) прямого угла.
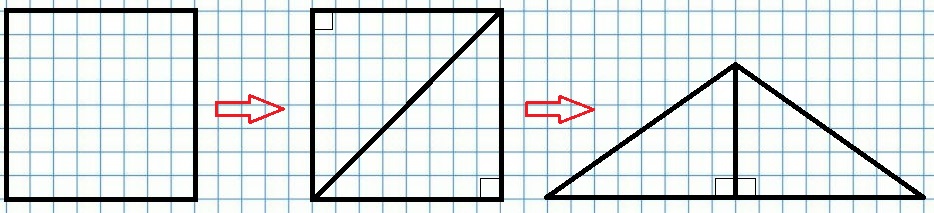
14. Начерти квадрат со стороной 4 см. Разбей этот квадрат на два прямоугольных треугольника. Составь из этих треугольников равнобедренный треугольник с основанием 8 см. Покажи на чертеже, как это сделать.
15. Методом подбора определи, какими могут быть длина и ширина прямоугольника, если его площадь равно 20 кв. см. Построй треугольник с площадью 10 кв. см.
Произведение длин сторон прямоугольника должно быть равно 20 кв. см. Это могут быть: 1 см и 20 см, 2 см и 10 см, 4 см и 5 см.
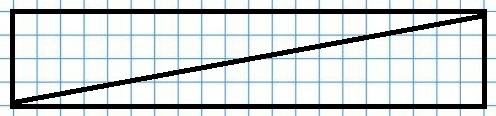
Прямоугольник со сторонами 2 см и 10 см имеет площадь 20 кв. см. Диагональ делит его на два равных одинаковых треугольника, следовательно каждый из двух треугольников имеет площадь 10 кв. см.
| ← Предыдущее | Следующее → |
Ответы к заданиям. Математика. Учебник. Часть 1. Чекин А.Л. 2012 г.
