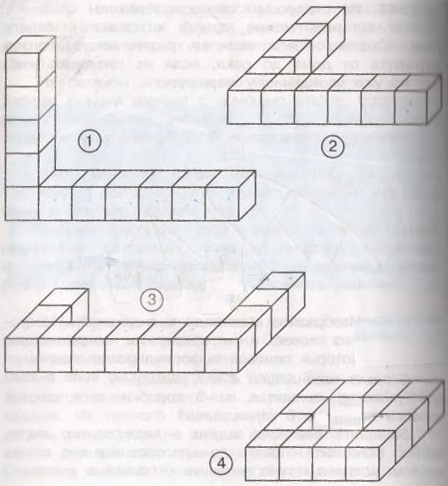
Разные задачи
Ответы к с. 99
342. На четырёх автоматических линиях расфасовывали конфеты в упаковки по 300 г. На одной линии произошёл сбой, и упаковки стали получаться по 330 г. Как с помощью одного взвешивания определить, на какой линии произошёл сбой?
Необходимо взять для взвешивания с первой линии 1 пакет, со второй линии — 2 пакета, с третьей линии — 3 пакета, с четвёртой линии — 4 пакета.
1) 1 + 2 + 3 + 4 = 10 (п.) — взяли всего для взвешивания
2) 300 • 10 = 3000 (г) — вес пакетов по норме
3) 330 — 300 = 30 (г) — больше в одном пакете от нормы
После взвешивания отобранных пакетов необходимо вычесть из их массы вес пакетов по норме и разделить полученную разность на 30 — полученное число и будет номером линии, на которой произошёл сбой.
343. На следующей схеме изображены тропинки, по которым можно пройти от дома к берегу реки. Сколько всего имеется различных вариантов маршрута от дома до реки, если не проходить ещё раз по уже пройденному маршруту.
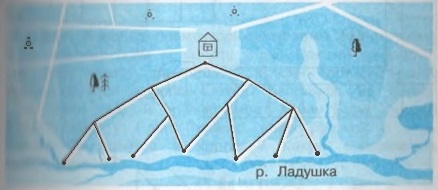
Необходимо подсчитать количество точек на берегу реки — их семь. Теперь нужно подсчитать количество отрезков из этих точек — их девять. Получается, что существует 9 возможных маршрутов, по которых можно от дома добраться до берега реки. Число точек на берегу реки (их 7), меньше, чем число маршрутов (их 9), так как к одной и той же точке в двух случаях из семи ведут два маршрута.
344. Изобразите в тетради в виде схемы, состоящей из точек и отрезков, их соединяющих, ситуацию, которая описана в формулировке задачи.
Сколько карандашей в 2-х упаковках, если в каждой упаковке находится по 3 коробки, а в каждой коробке лежит по 6 карандашей?
Запишите решение задачи в виде одного выражения. Вычислите ответ задачи и сравните его с тем числом, которое можно получить с помощью схемы.
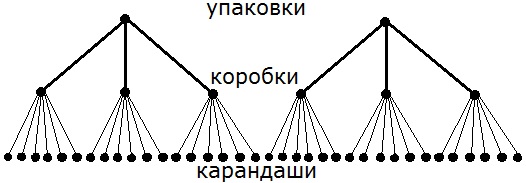
2 • 3 • 6 = 36 (к.)
О т в е т: 36 карандашей.
Ответы к заданиям. Математика. Учебник. Часть 1. Чекин А.Л. 2012 г.
Математика. 4 класс. Чекин А.Л.