Декабрь | 2018 | | Умники и умницы

Ответы к с. 90

307. Для построения следующих фигур использовались одинаковые кубики. Назови номер фигуры, которая имеет наименьший объём, и номер фигуры, которая имеет наибольший объём.

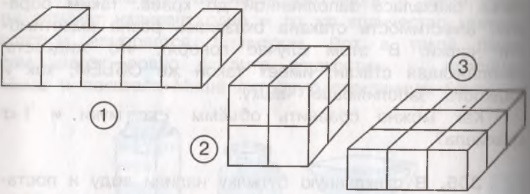
Рисунок к заданию 307 стр. 90 учебник часть 1 по математике 4 класс Чекин

Фигура 1 составлена из 7 кубиков, фигура 2 составлена из 8 кубиков, фигура 3 составлена из 9 кубиков. При условии, что все кубики одинаковые, бóльший объём будет иметь фигура, составленная из бóльшего количества кубиков. Следовательно, наибольший объём имеет фигура 3, а наименьший объём – фигура 1.

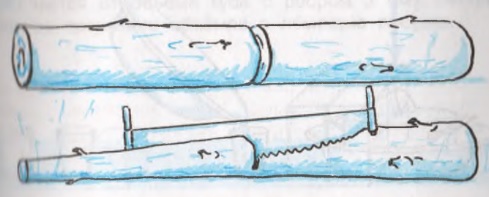
308. В большую кастрюлю, стоящую в тазу, до самого края налили воду, а потом опустили в неё кирпич. В результате часть воды вытекла в таз. Что ты можешь сказать об объёме кирпича и объёме вытесненной им воды?

Объём погруженного в воду предмета произвольной формы, например, кирпича, равен объёму вытесненной им жидкости. То есть, если вытесненную жидкость собрать и измерить её объём, то таким же будет объём предмета.

309. Опишите по рисунку практическую работу, по результатам которой можно сравнить вместимость стакана и его объём (как реального предмета).

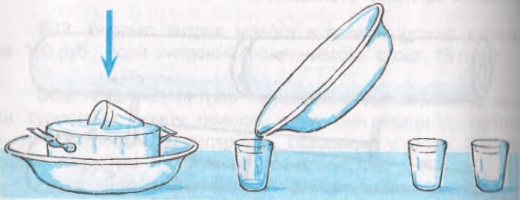
Рисунок к заданию 309 стр. 90 учебник часть 1 по математике 4 класс Чекин

Полностью погружаем стакан в кастрюлю (без воздушных пробок), до краёв наполненную водой, которая стоит в тазу. Наблюдаем, как по мере погружения стакана, вода, вытесняемая стаканом, выливается в таз. Вытаскиваем заполненный водой стакан из кастрюли, а кастрюлю из таза и аккуратно переливаем воду из таза в такой же стакан. Наблюдаем, что стакан заполнится водой частично. Выставляем два одинаковых стакана: один заполнен водой полностью, второй – частично (вода, собранная из таза). Вспоминаем, что объём воды в первом стакане, равен вместимости этого стакана, объём воды во втором стакане равен объёму стеклянных стенок и дна этого стакана. Делаем вывод, что вместимость стакана больше его объёма.

Вместимость и объём

Ответы к с. 89

304. Когда Миша взял стакан, заполненный молоком, и перелил всё молоко в чашку, то она также оказалась заполненной до краёв. Таким образом, вместимость стакана оказалась равна вместимости чашки. В этом случае говорят, что жидкость, заполняющая стакан, имеет такой же ОБЪЁМ, как и жидкость, заполняющая чашку.
Как можно сравнить объёмы 1 кг муки и 1 кг крахмала?

Необходимо насыпать 1 кг муки и 1 кг крахмала в одинаковые ёмкости, например, в двухлитровые банки. Разравнять ложкой или лопаткой поверхность муки и крахмала в банках. Провести измерение: 1 кг муки будет занимать меньше пространства в банке, чем 1 кг крахмала. Получается, что объём 1 кг муки меньше объёма 1 кг крахмала.

305. В стеклянную бутылку налили воду и поставили на мороз. Ты уже знаешь, что, когда вода замёрзнет, бутылка лопнет. Попробуй дать объяснение этого факта на основе сравнения объёмов воды и льда, получившегося из этой воды.

Вместимость бутылки равна объёму воды, которая её заполняет. Образовавшийся из воды лёд увеличился в объёме и разбил бутылку. Следовательно, объём льда больше объёма бутылки (лёд не помещается в бутылке) и больше объёма воды (которая помещалась в бутылке).

306. Круглое бревно, толщина котрого по всей длине одинакова, распилили пополам по длине. Сравни объёмы получившихся частей.
Изменится ли ответ, если бревно от одного конца к другому утолщается?

Рисунок к заданию 306 стр. 89 учебник часть 1 по математике 4 класс Чекин

Части распиленного бревна имеют цилиндрическую форму, и они одинаковы по толщине и по длине. Если представить, что половинки бревна являются сосудами цилиндрической формы, то объём жидкости, вмещающейся в эти сосуды будет одинаковым. Следовательно, объёмы этих половинок бревна будут одинаковые. Если же бревно утолщается от одного конца к другому, то по длине его половинки будут одинаковые, а по толщине части распиленного бревна будут разными. Если представить части этого бревна в виде сосудов конусовидной формы, то жидкость, заполняющая более «тонкую» часть сосуда, будет занимать меньший объём. Следовательно, объёмы таких частей бревна будут разными.

← Предыдущее

Следующее →

Ответы к заданиям. Математика. Учебник. Часть 1. Чекин А.Л. 2012 г.

Математика. 4 класс. Чекин А.Л.