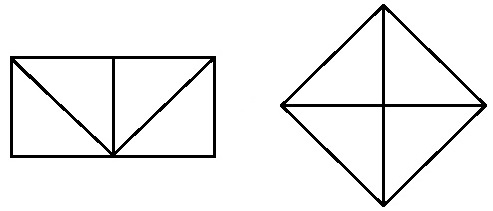
Равносоставленные и равновеликие фигуры

Ответы к с. 130

395. Выбери два треугольника, из которых можно составить прямоугольник.
Начерти составленный прямоугольник.
Во сколько раз нужно уменьшить площадь прямоугольника, чтобы получить площадь одного из выбранных треугольников?

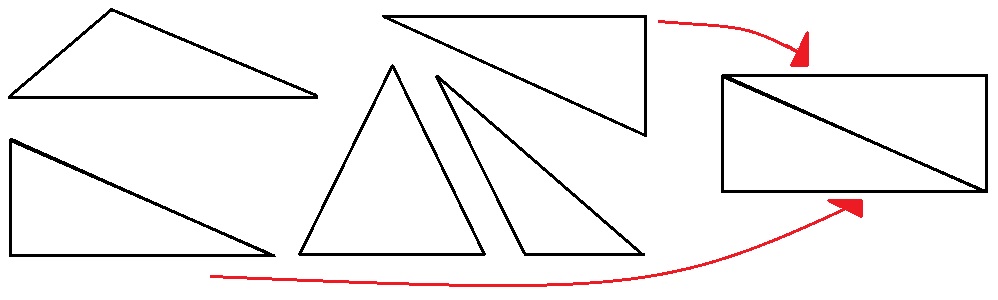
Поскольку прямоугольник состоит из двух одинаковых прямоугольных треугольника, то площадь прямоугольника нужно уменьшить в 2 раза.

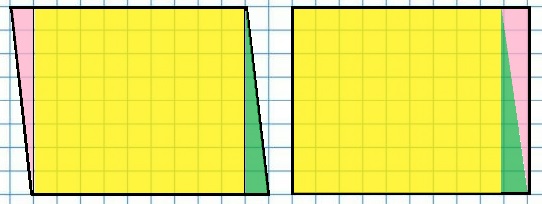
396. Начерти прямоугольник, который состоит из двух данных одинаковых прямоугольников.
Можно ли предложить другой вариант решения этой задачи? Сравни свой вариант решения с вариантом решения соседа по парте.

Данная задача имеет только один вариант решения, поскольку при размещении прямоугольников друг над другом получается квадрат.

Ответы к заданиям. Математика. Учебник. Часть 2. Чекин А.Л. 2013 г.

Математика. 3 класс. Чекин А.Л.

Равносоставленные и равновеликие фигуры

Ответы к с. 129

393. Начерти одну пару равносоставленных фигур. Что ты можешь сказать о площади этих фигур?
Могут ли равносоставленные фигуры иметь разную площадь?
Сформулируй свойство равносоставленных фигур, используя ещё и термин РАВНОВЕЛИКИЕ ФИГУРЫ, которым называют фигуры с одинаковой площадью.

Поскольку обе фигуры состоят из четырёх одинаковых равносторонних прямоугольных треугольника, то и площади их равны. Таким образом, равносоставленные фигуры не могут иметь разную площадь. Поэтому они ещё называются равновеликими, то есть равносоставленные фигуры — ещё и равновеликие.

394. Используя свойство, которое состоит в том, что равносоставленные фигуры являются равновеликими, докажи, что площади данных четырёхугольников равны.
Для этого раздели первую фигуру на части так, чтобы из них можно было бы составить вторую.

Ответы к заданиям. Математика. Учебник. Часть 2. Чекин А.Л. 2013 г.

Математика. 3 класс. Чекин А.Л.