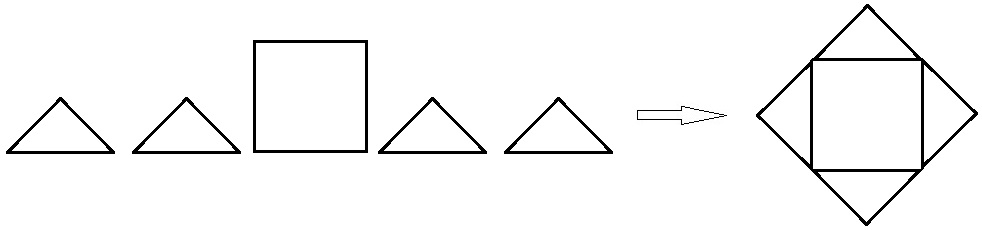
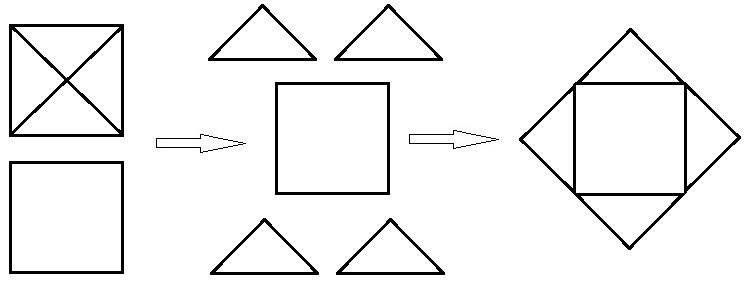
Равносоставленные и равновеликие фигуры

Ответы к с. 129

393. Начерти одну пару равносоставленных фигур. Что ты можешь сказать о площади этих фигур?
Могут ли равносоставленные фигуры иметь разную площадь?
Сформулируй свойство равносоставленных фигур, используя ещё и термин РАВНОВЕЛИКИЕ ФИГУРЫ, которым называют фигуры с одинаковой площадью.

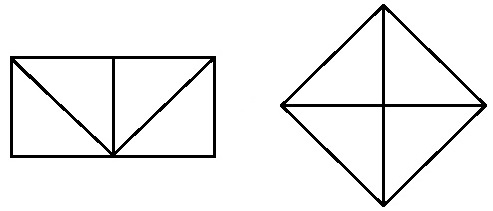
Поскольку обе фигуры состоят из четырёх одинаковых равносторонних прямоугольных треугольника, то и площади их равны. Таким образом, равносоставленные фигуры не могут иметь разную площадь. Поэтому они ещё называются равновеликими, то есть равносоставленные фигуры — ещё и равновеликие.

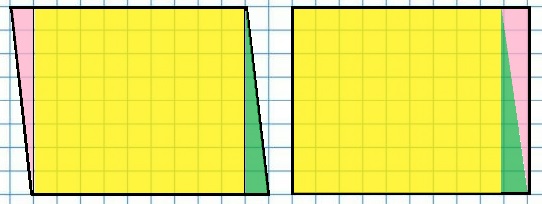
394. Используя свойство, которое состоит в том, что равносоставленные фигуры являются равновеликими, докажи, что площади данных четырёхугольников равны.
Для этого раздели первую фигуру на части так, чтобы из них можно было бы составить вторую.

Ответы к заданиям. Математика. Учебник. Часть 2. Чекин А.Л. 2013 г.

Математика. 3 класс. Чекин А.Л.

Составление и разрезание фигур

Ответы к с. 128

390. Из квадрата и четырёх равных прямоугольных равнобедренных треугольников, изображённых на рисунке составь квадрат.

391. Из двух равных квадратов составь новый квадрат, предварительно разрезав один из данных квадратов на четыре части.
Во сколько раз площадь нового квадрата будет больше площади одного из данных квадратов?

Новый квадрат составлен из двух одинаковых квадратов, следовательно, его площадь будет в 2 раза больше больше площади одного из исходных квадратов.

392. Данный четырёхугольник разрежь на две части, из которых можно составить треугольник. Покажи с помощью чертежа, как это сделать.

Ответы к заданиям. Математика. Учебник. Часть 2. Чекин А.Л. 2013 г.

Математика. 3 класс. Чекин А.Л.